[트랜스포머 뜯어보기-2] Self-Attention 이해하기

앞서 트랜스포머의 전체적인 구조에 관해 알아보았습니다. 그러면서 트랜스포머는 Recurrence, Convolution 연산 대신에 Self-Attention 연산만을 사용한다는 점을 짚었는데요. 짐작하셨겠지만 Self-Attention 연산은 트랜스포머를 알고자 한다면 필히 공부해야 할 주요 부품입니다.

1. Self-Attention 연산의 전체적인 구조

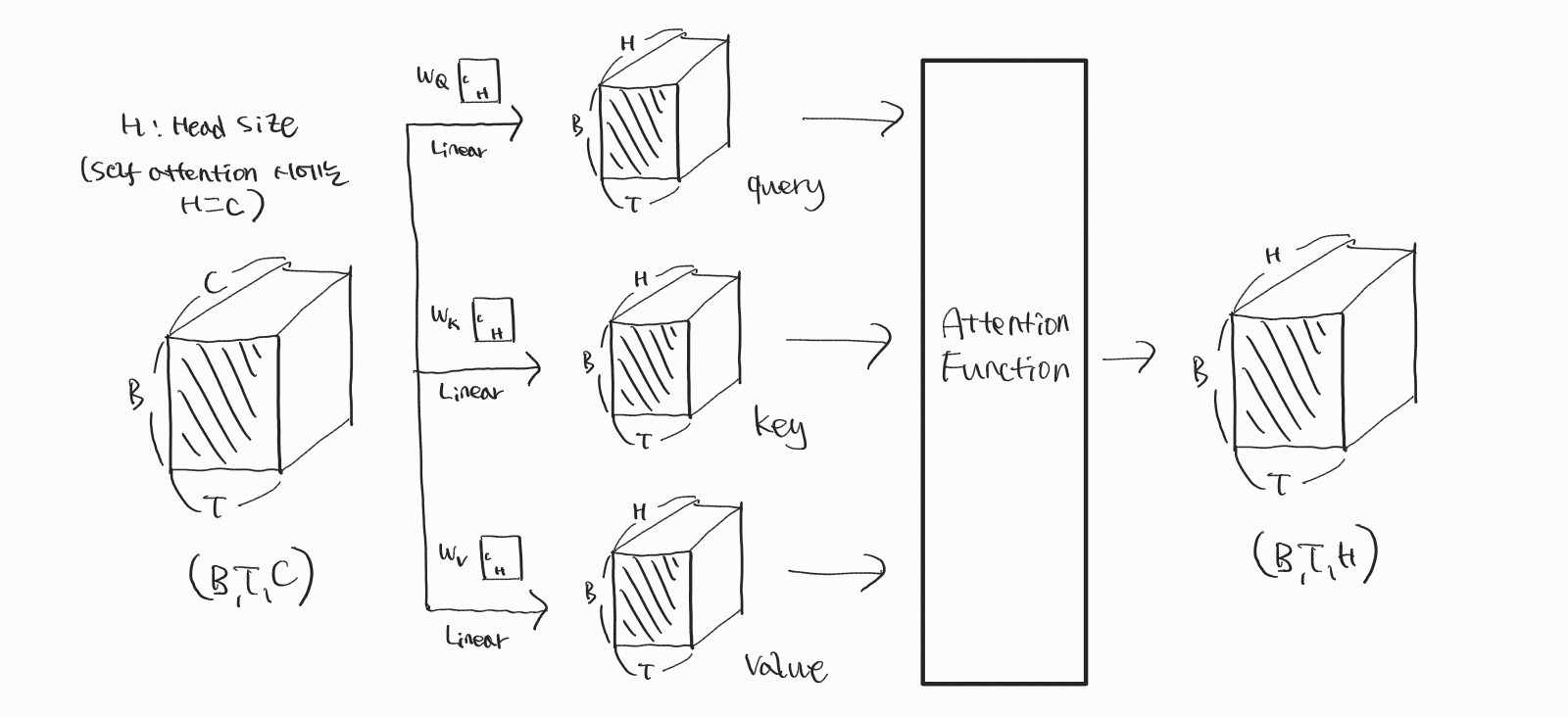
위의 그림은 Self-Attention 연산에 관한 이해를 돕기 위해 직접 그린 그림입니다. 맨 왼쪽에 (B, T, C)라고 쓰여진 직육면체 한 개가 있는 것이 보이실 텐데요. 직육면체는 Self-Attention 연산을 하기 위해 들어가는 Input 행렬이고, 3개 차원을 가지며 행렬의 사이즈가 (B, T, C)입니다. 첫 번째 차원은 배치 번호를 나타내며, 배치의 개수는 총 B개입니다. 두 번째 차원은 시점 번호를 나타내며, 시점의 개수, 즉 하나의 배치당 토큰의 개수는 총 T개입니다. 세 번째 차원은 각 토큰을 C차원의 벡터로 토큰 임베딩을 해주며 만들어진 차원입니다. 아래 그림이 이해를 도울 것입니다.

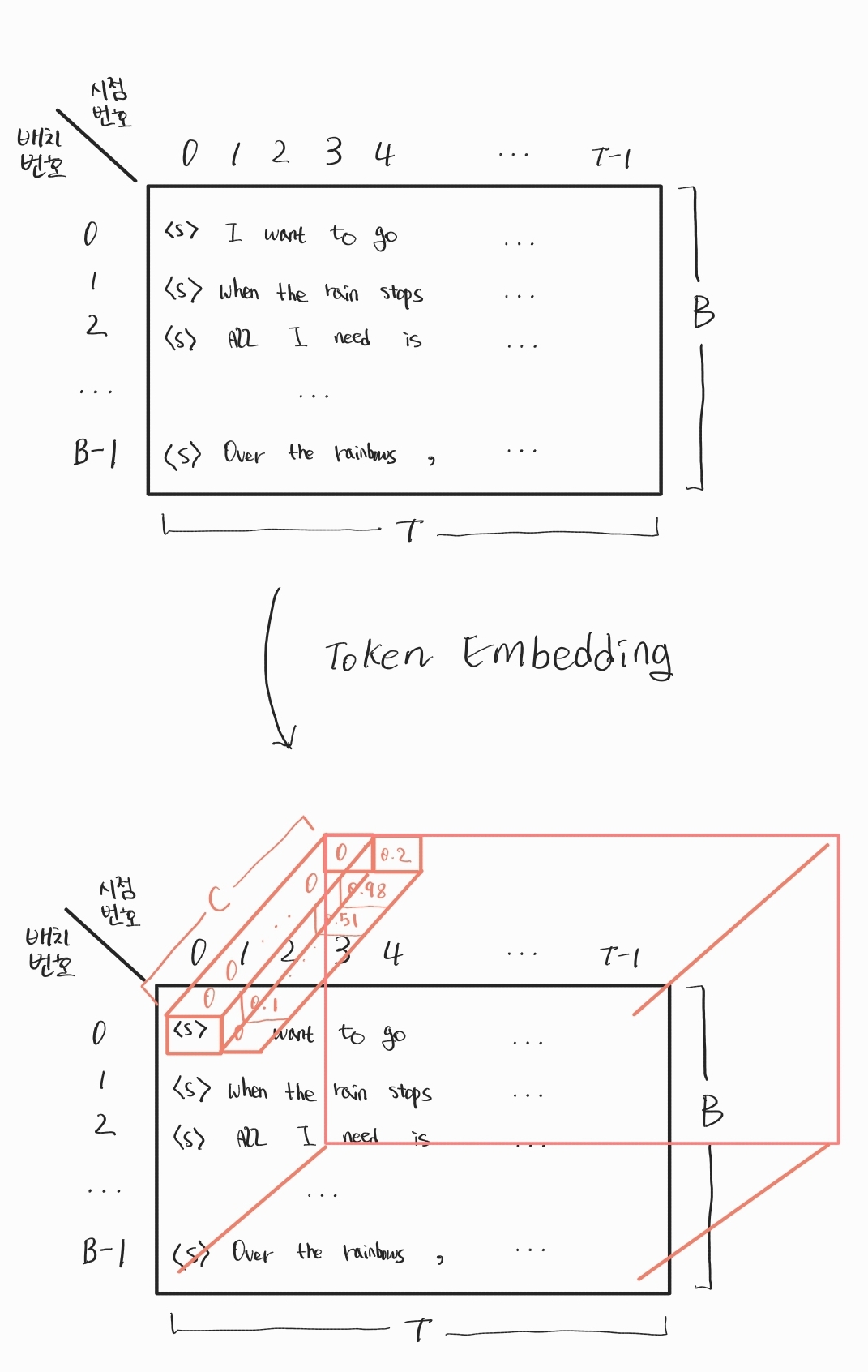
직육면체의 의미를 이해했다면 다시 그림을 살펴보겠습니다.

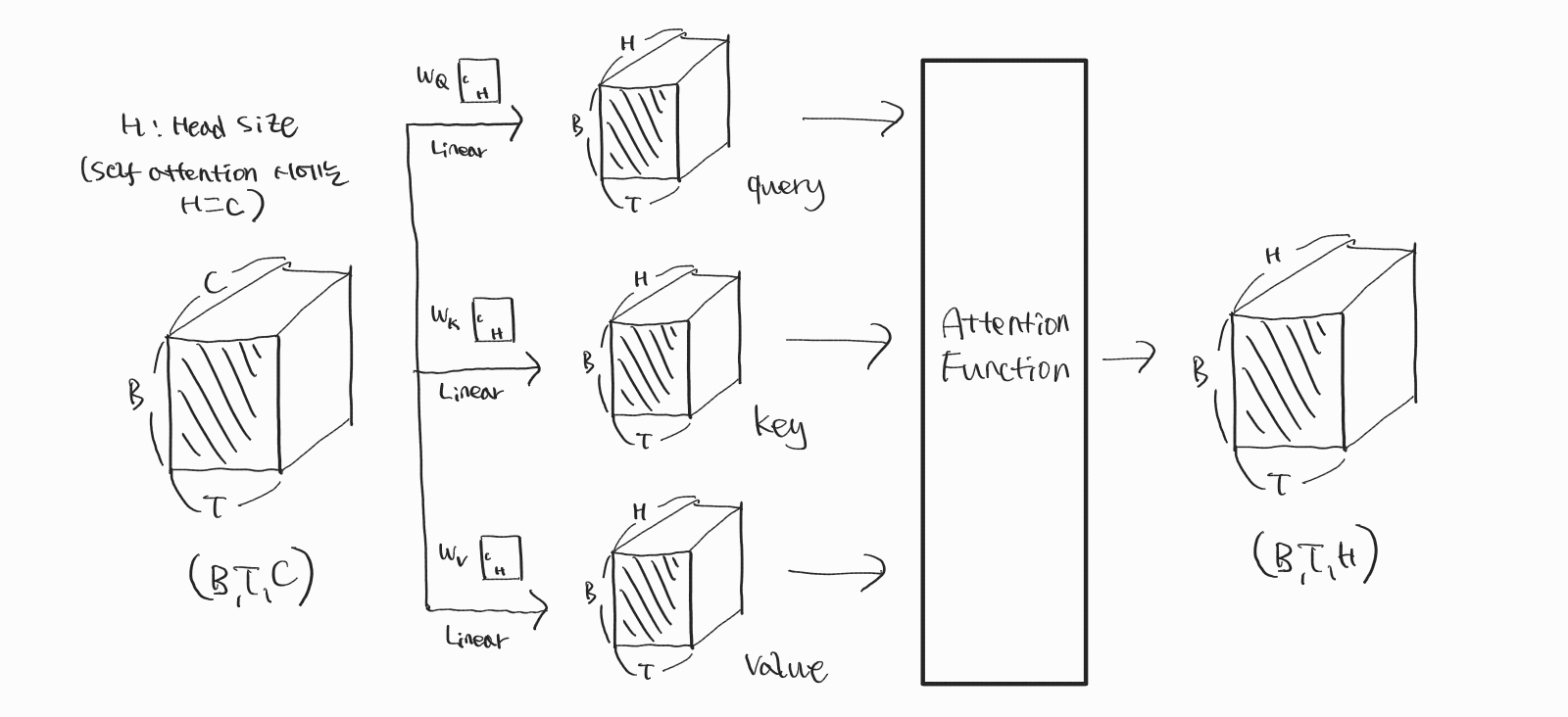
(B, T, C)의 크기를 가지는 입력 행렬로부터 (B, T, H)의 크기를 가지는 행렬 3개가 만들어지는 것을 확인할 수 있습니다. 이 세 개의 (B, T, H) 행렬은 (B, T, C) 입력 행렬과 (C, H) 가중치 행렬의 행렬곱을 통해 만들어진 것입니다. 이 세 개의 행렬을 쿼리(Query, $Q$), 키(Key, $K$), 밸류(Value, $V$)라고 부릅니다. $Q$, $K$, $V$를 생성하고 나면, attention 함수로 연산을 진행하여 (B, T, H) 크기의 행렬을 반환하게 됩니다. 이 (B, T, H) 행렬이 self-attention 연산의 출력이 됩니다.

$Q$, $K$ 그리고 $V$ 세 개의 행렬은 각각 서로 다른 세 개의 (C, H) 가중치 행렬 $W_q$, $W_k$, $W_v$로부터 생성됩니다. $W_q$, $W_k$, $W_v$ 세 개의 가중치 행렬들은 훈련이 이루어지면서 오차의 역전파를 통해 제각기 업데이트됩니다.

요약하자면, self-attention은 입력 행렬을 서로 다른 세 개의 가중치 행렬 $W_q$, $W_k$, $W_v$과 각각 행렬곱하여 쿼리(Query, $Q$), 키(Key, $K$), 밸류(Value, $V$) 3개의 행렬을 만들어내고, 이 값들을 attention 함수에 넣고 계산한 결과를 반환합니다. 그렇다면 쿼리, 키, 밸류 행렬이 무엇을 의미하는지, attention 함수는 어떤 함수인지 이어서 살펴보겠습니다.

2. Attention 함수는 어떤 함수?

트랜스포머의 특별한 Attention 함수 = Scaled Dot-Product Attention!

사실, Attention 함수는 하나로 정해져 있는 것이 아닙니다. 여러 Attention 함수들 중 하나를 선택해서 사용할 수 있습니다. 논문 Attention is All You Need에서 제안한 트랜스포머 모델에서는 Attention 함수들 중 Scaled Dot-Product Attention 함수를 사용합니다. Scaled Dot-Product Attention 함수를 이해하기 위해, 먼저 Dot-Product Attention 함수부터 살펴보겠습니다.

아래 수식이 바로 Dot-Product Attention 함수의 수식입니다.

$y = Softmax(Q \cdot K^T)\cdot V$

$Q$, $K$, $V$는 위에서 설명한 쿼리, 키, 밸류 행렬을 의미하며, $K^T$는 키 행렬의 전치행렬을 나타냅니다. 쿼리와 키 전치행렬을 Dot-Product한 후 Softmax를 취한 결과를 다시 밸류 행렬과 Dot-Product를 한 것이 Dot-Product Attention 함수의 출력값이 됩니다.

아래 수식은 Scaled Dot-Product Attention 함수의 수식입니다.

$y = Softmax(\frac{Q \cdot K^T}{\sqrt{d_k}})\cdot V$

방금 전에 보여준 Dot-Product Attention 함수식과 무엇이 다른지 찾아낼 수 있겠죠? Dot-Product Attention 함수에서 딱 한 가지 과정만 추가되었습니다. Softmax를 취하기 전에 쿼리와 키 전치행렬을 Dot-Product한 값을 $\sqrt{d_k}$로 나누어 주는 과정만 추가되었습니다. 이 과정을 ‘Scaling’이라고 부릅니다.

Scaling이 대체 뭘 하는 과정인지 간략히 살펴보겠습니다. 만약 $Q$, $K$가 $mean=0$, $variance=1$을 가지는 독립적인 변수라고 한다면, $Q \cdot K$는 $mean=0$, $variance=d_k$를 가지게 될 것인데요. $Q \cdot K$의 각 원소를 $\sqrt{d_k}$로 나누는 Scaling 과정을 거치게 되면, $Q \cdot K$은 다시 $mean=0$, $variance=1$를 가지게 될 것입니다. 이처럼 Scaling 과정은 데이터의 분산(Variance)을 줄이는, 즉 데이터의 분포를 고르게 만들어주는 과정입니다. 데이터의 분산이 너무 크게 되면 데이터의 분포가 고르지 못하게 될 것이고, 이렇게 되면 $Q \cdot K$의 원소 중에서 다른 원소에 비해 크기가 상대적으로 크거나 작은 원소들의 힘이 너무 세질 수 있는데요. 이를 방지하고 $Q \cdot K$의 각 원소들이 훈련 과정에 끼치는 영향을 어느 정도 고르게 만들기 위하여 Scaling을 하는 것입니다.

Scaled Dot-Product Attention 함수의 실행 과정 시각적으로 이해하기!

이번에는 Scaled Dot-Product Attention 함수의 실행 과정을 그림을 통해 살펴보겠습니다.

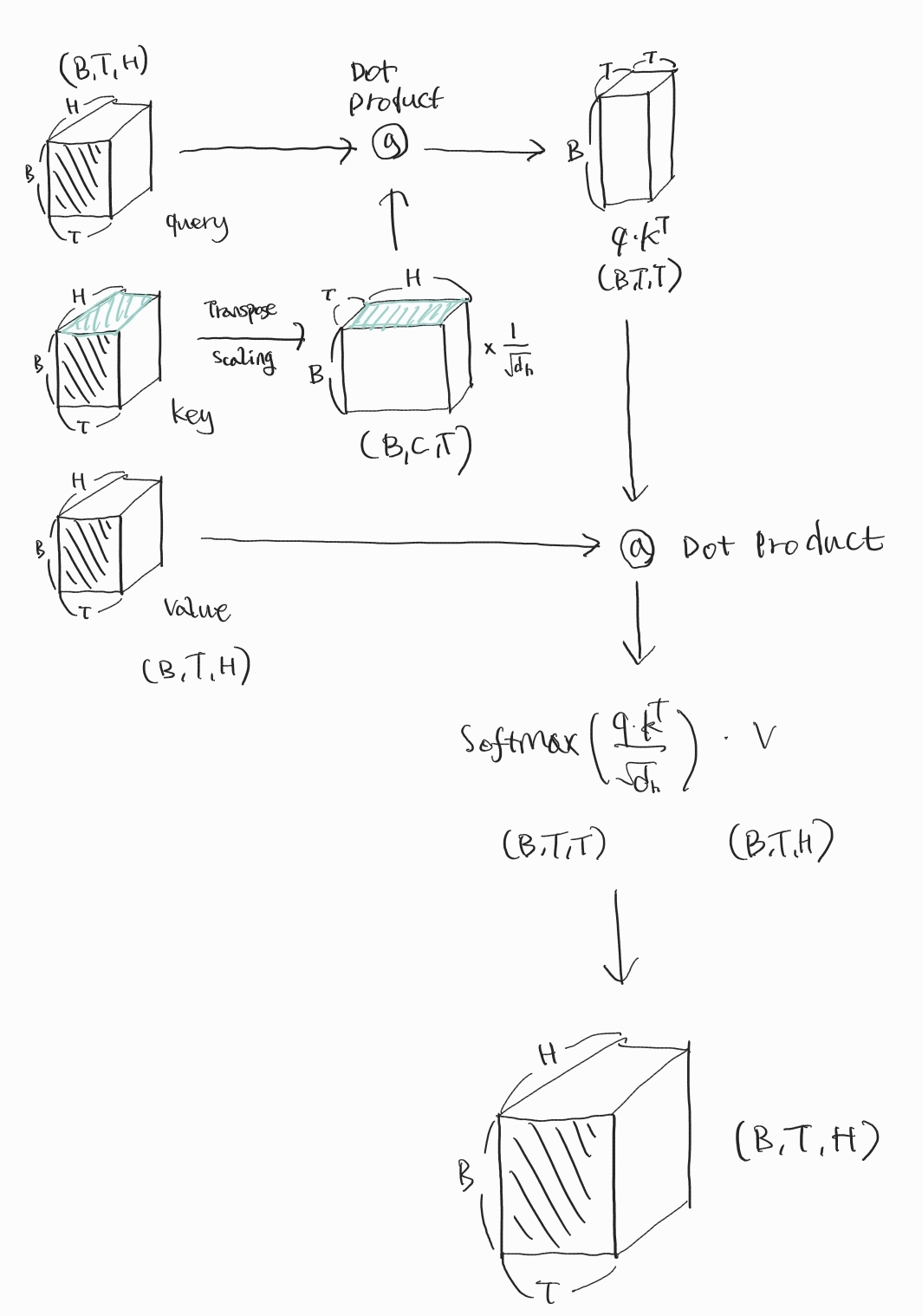
앞서 B는 배치의 개수, T는 시점(토큰)의 개수, H는 은닉층에서의 벡터 차원이라고 말씀드렸습니다.(B, T, H)의 크기를 가지는 쿼리, 키, 밸류 행렬이 함수의 입력으로 들어가고, 똑같이 (B, T, H)의 크기를 가지는 행렬이 함수의 출력으로 반환됩니다.

$y = Softmax(\frac{Q \cdot K^T}{\sqrt{d_k}})\cdot V$

위 수식과 같이, 쿼리와 키 전치행렬을 Dot-Product한 값에 Scaling을 해주고, 이를 다시 밸류 행렬과 Dot-Product합니다. 그림에서는 키 전치행렬을 Dot-Product하기 전에 미리 Scaling을 하는데 이 순서는 바뀌어도 똑같은 결과를 낳으니 혼동하지 않으시길 바랍니다.

Masking 과정을 추가한 Scaled Dot-Product Attention

이번에는 위에서 공부한 Scaled Dot-Product Attention 함수에 Masking 과정을 추가한 버전의 Attention 함수를 알아보겠습니다. 논문 Attention is All You Need에서 제안하는 트랜스포머 모델에서는 Masking 과정을 거치는 버전의 Attention 함수와 거치지 않는 버전의 Attention 함수를 둘 다 이용합니다. 그러니 두 버전의 Attention 함수를 모두 이해하고 구분할 줄 알아야 합니다.

Masking 과정을 거치지 않는 버전의 Attention 함수를

$y = Softmax(\frac{Q \cdot K^T}{\sqrt{d_k}})\cdot V = Softmax(Scaling(Q \cdot K^T)\cdot V$ 라고 한다면,

Masking 과정을 거치는 버전의 Attention 함수는

$y = Softmax(W \cdot \frac{Q \cdot K^T}{\sqrt{d_k}})\cdot V = Softmax(Masking(Scaling(Q \cdot K^T))\cdot V$입니다.

무엇이 달라졌을까요? Scaling 과정을 거친 후 $W$라는 가중치 행렬에 행렬곱을 해주는 ‘Masking’ 과정이 추가되었습니다. Masking 과정에서의 가중치 행렬 $W$는 훈련을 거치며 업데이트되는 행렬이 아니라 값이 정해져 있는 상수와 같습니다.

$W = \left[ \begin{matrix} 1 & 0 & 0 & 0 & \cdots & 0 \\ 1/2 & 1/2 & 0 & 0 & \cdots & 0 \\ 1/3 & 1/3 & 1/3 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1/T & 1/T & 1/T & 1/T & \cdots & 1/T \end{matrix} \right]$

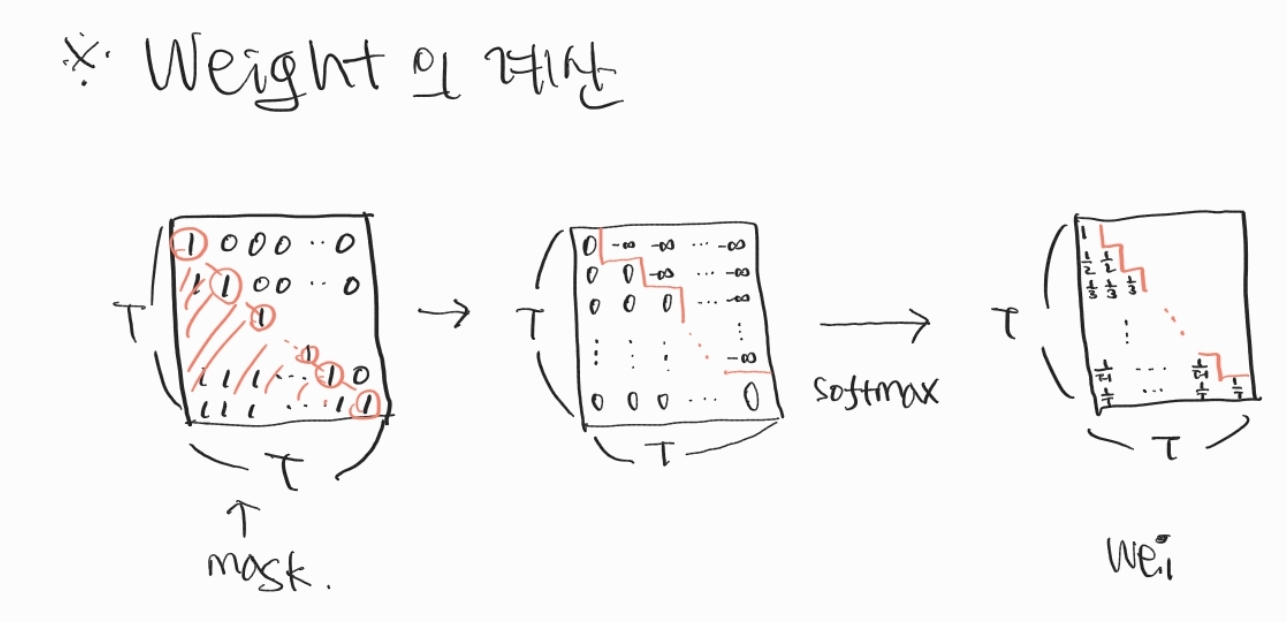
이 행렬을 만들 때는 위 그림과 같은 방식으로 만들 수 있습니다. 위의 그림에 나오는 ‘Wei’ 행렬은 $W$와 같습니다.

$w = \left[ \begin{matrix} 0 & -\infty & -\infty & -\infty & \cdots & -\infty \\ 1 & 1 & -\infty & -\infty & \cdots & -\infty \\ 1 & 1 & 1 & -\infty & \cdots & -\infty \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & 1 & 1 & \cdots & 1 \end{matrix} \right]$

바로 위와 같은 행렬에 Softmax를 취해주는 것입니다.

$W = \left[ \begin{matrix} 1 & 0 & 0 & 0 & \cdots & 0 \\ 1/2 & 1/2 & 0 & 0 & \cdots & 0 \\ 1/3 & 1/3 & 1/3 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1/T & 1/T & 1/T & 1/T & \cdots & 1/T \end{matrix} \right] = Softmax\left( \left[ \begin{matrix} 0 & -\infty & -\infty & -\infty & \cdots & -\infty \\ 1 & 1 & -\infty & -\infty & \cdots & -\infty \\ 1 & 1 & 1 & -\infty & \cdots & -\infty \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & 1 & 1 & \cdots & 1 \end{matrix} \right] \right)$

Masking을 통해 무엇을 얻을 수 있는지는 잠시 후 살펴보겠습니다.

Masked Scaled Dot-Product Attention 함수의 실행 과정 시각적으로 이해하기!

그전에 Masking 과정을 포함하는 Scaled Dot-Product Attention 함수의 실행 과정을 그림을 통해 살펴보겠습니다.

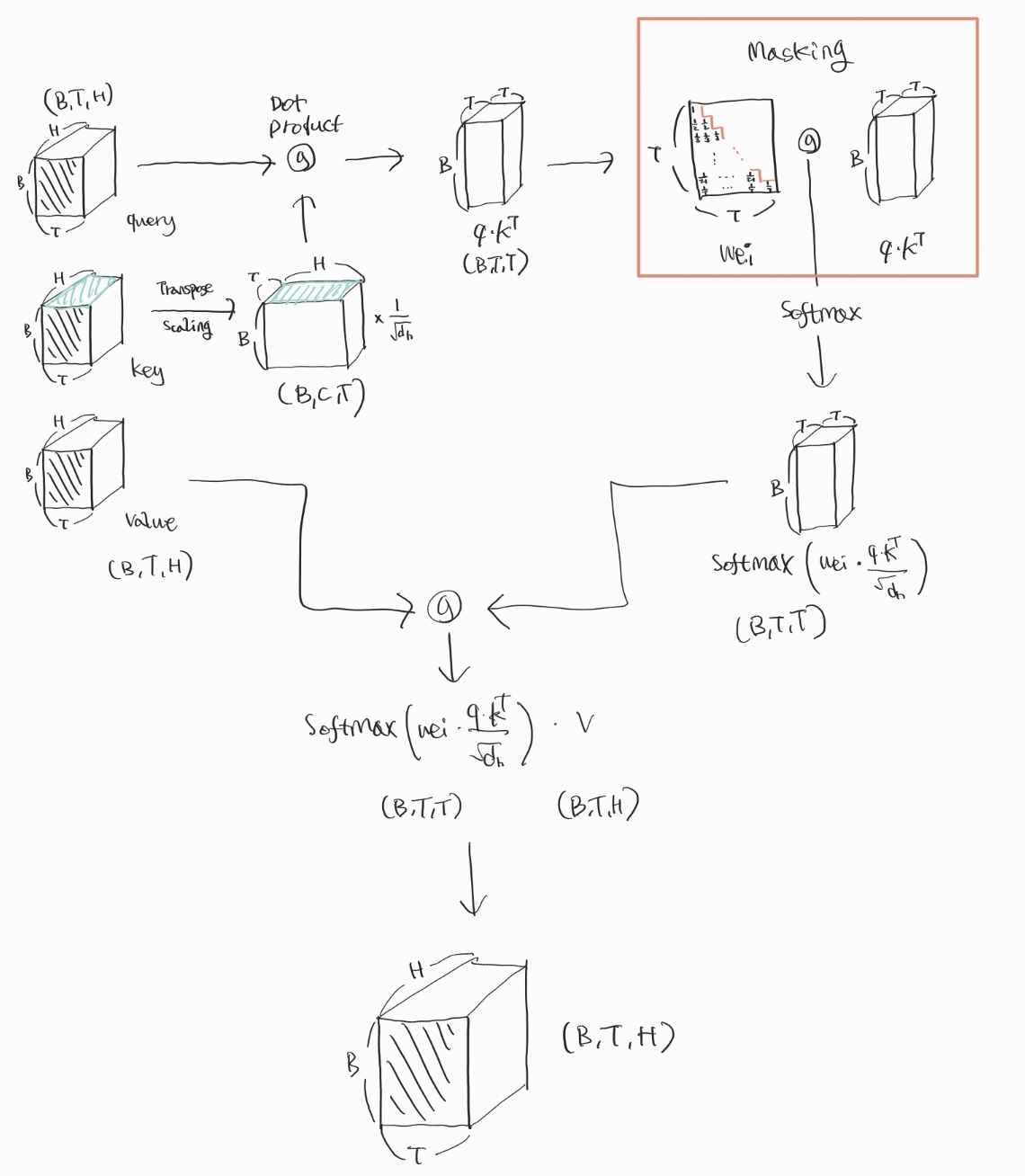
Scaling 과정을 거친 후 Wei라고 쓰여 있는 $W$ 행렬과의 행렬곱을 통해 Masking 과정을 거치는 것을 그림을 통해 확인할 수 있습니다.

3. Attention 함수 이해하기

드디어 마지막 파트입니다. 이 부분이 마지막 파트이자 이 글의(어쩌면 이 시리즈의?) 화룡점정입니다. 여기에서는 Masked Scaled Dot-Product Attention 함수의 내부를 뜯어보면서 ‘Attention’의 의미를 이해하고자 합니다.

지금까지는 Attention 함수를 실행할 때 (B, T, C)의 크기를 가지는 3차원 행렬 쿼리, 키, 밸류를 가지고 연산하는 것으로 배웠습니다. 이번에는 Attention 함수에 대해 더 깊이 이해할 수 있도록, Attention 함수의 동작을 배치별로 나누어서 살펴보겠습니다. 이렇게 하면 같은 배치로부터 얻은 쿼리, 키, 밸류 값이 서로 어떻게 얽혀서 연산이 일어나는지 이해할 수 있을 것입니다.

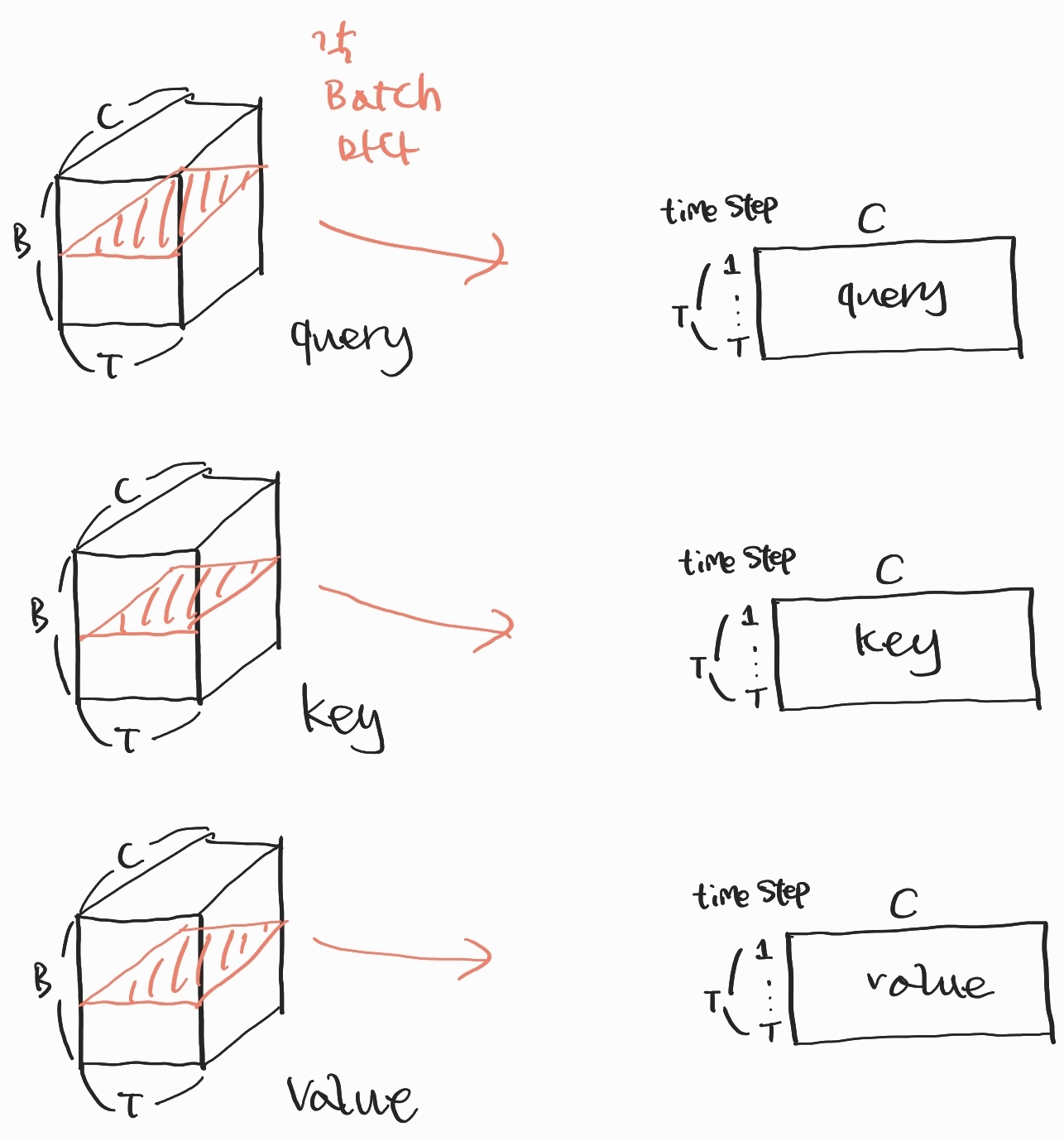
위 이미지는 특정 배치에서의 쿼리, 키, 밸류 값을 (T, C)의 크기를 갖는 2차원 행렬로 나타낸 것입니다. 예를 들어 1번째 배치에서의 동작을 살펴보고자 한다면, 쿼리, 키, 밸류 각각의 행렬에서 배치 차원 0번째 인덱스에 해당하는 (T, C) 2차원 행렬을 각각 뽑아낸 것입니다.

특정 배치를 지정해두고 뽑아낸 2차원 쿼리, 키, 밸류 행렬들을 살펴보겠습니다. 이들은 T개의 토큰 각각과 대응되는 C차원 벡터들을 쌓아 놓은 형태처럼 보입니다. 그러니까, 쿼리 행렬에서 t번째 행벡터는 t번째 토큰의 쿼리(C차원)라고 생각할 수 있겠죠. 마찬가지로 키 행렬에서 t번째 행벡터는 t번째 토큰의 키입니다. 밸류 행렬에서 t번째 행벡터는 t번째 토큰의 밸류고요.

그렇다면 현재의 배치에서 쿼리와 키 치환행렬 사이의 행렬곱은 어떤 의미를 가질까요?

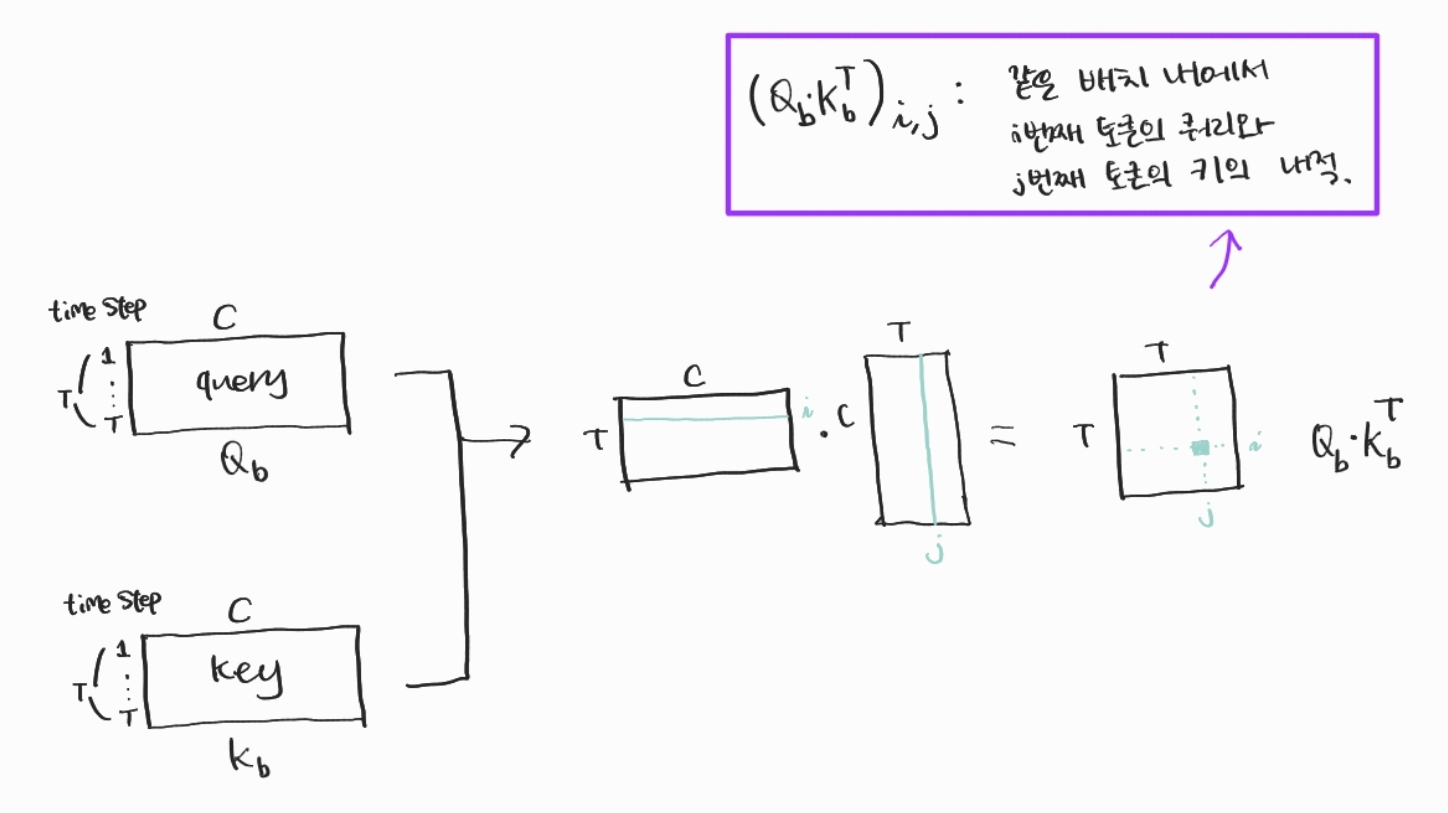
위 그림처럼, 현재의 배치에서 쿼리와 키 치환행렬의 행렬곱을 계산하면 (T, T)의 크기를 가지는 2차원 행렬이 나옵니다. 이 행렬에서 i번째 행, j번째 열에 들어가는 값은 어떻게 얻어진 값일지 생각해봅시다. 이는 바로 쿼리 행렬의 i번째 행벡터와 키 행렬의 j번째 행벡터를 내적한 것입니다. 즉, i번째 토큰의 쿼리와 j번째 토큰의 키를 내적한 것이죠.

이것은 i번째 토큰과 관련된 예측을 하고자 할 때 j번째 토큰에 얼마나 주목(Attention)할 것인지를 나타내는 값으로 이해하면 됩니다.

데이터베이스에서 쿼리와 키의 의미를 아는 분이라면 더 직관적인 이해가 가능할 것입니다. i번째 토큰의 쿼리는 “나 i번째 토큰과 관련해서 예측을 좀 하려고 하는데 너를 어떻게 참조하면 될까?”라는 메시지를 전달하고, j번째 토큰의 키는 “j번째 토큰은 너를 이렇게 참조하면 될 것 같아”라는 답장을 한다고 생각하시면 됩니다. 쿼리와 키를 행렬곱이라는 계산을 통해 매칭시키면 말씀드린 대로 i번째 토큰과 관련된 예측을 하고자 할 때 j번째 토큰에 얼마나 주목(Attention)할지 알 수 있게 되는 것입니다.

정리하자면, 쿼리와 키 치환행렬의 행렬곱을 하면 2차원 (T, T) 행렬이 얻어지는데요. 이 행렬의 (i, j) 칸에는 i번째 토큰과 관련된 예측을 하고자 할 때 j번째 토큰에 얼마나 주목(Attention)할지를 나타내는 값이 들어갑니다. 로직상, (i, j) 칸에 들어가는 값이 클수록 많이 주목하게 되고, 작을수록 적게 주목하게 됩니다. 이쯤이면 Attention, 즉 주목한다는 것의 의미에 대해 감이 잡히셨길 바랍니다.

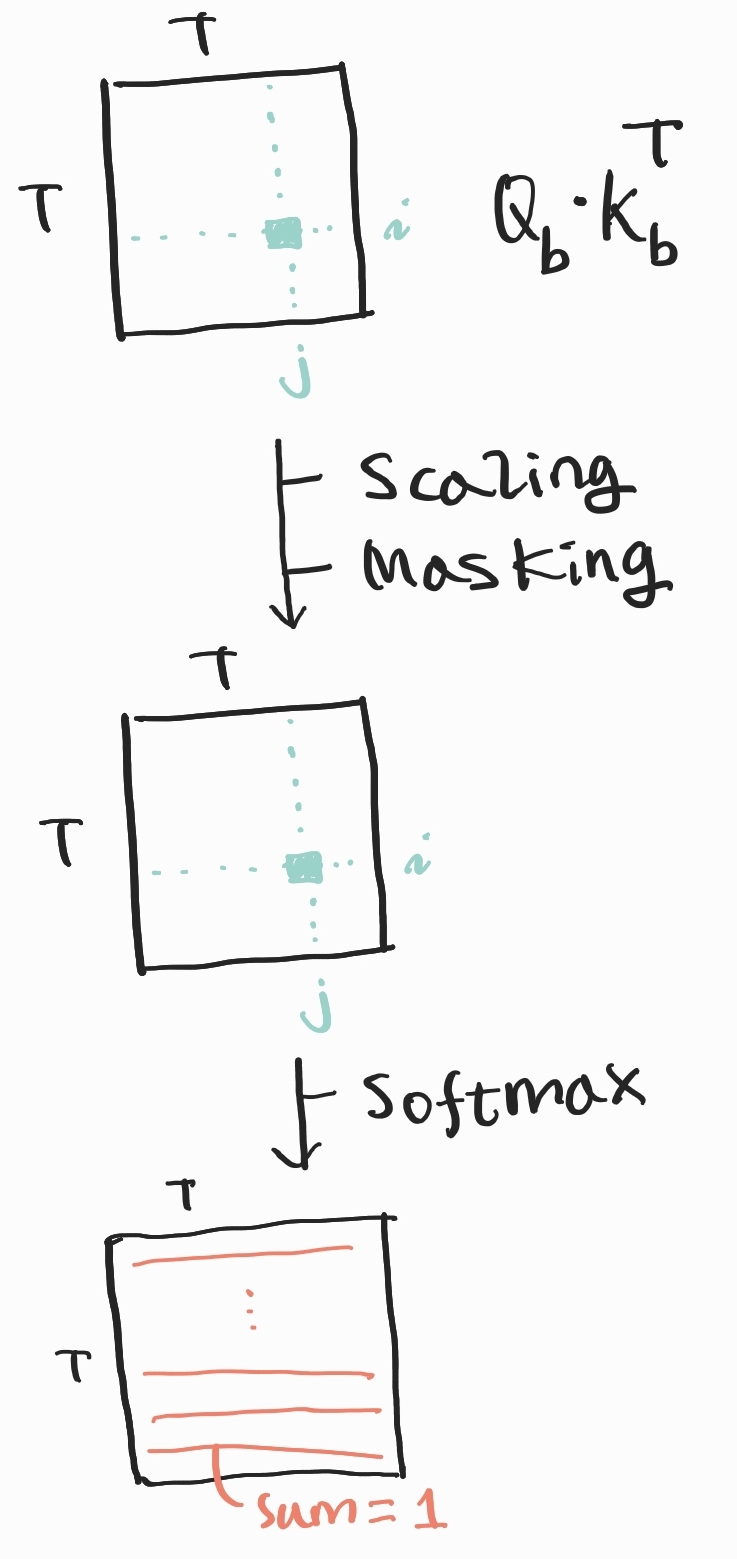
다음으로는 앞에서 구한 (T, T) 2차원 행렬에 차례대로 Scaling, Masking, Softmax 처리를 합니다. Scaling은 말씀드린대로 행렬의 모든 원소를 $d_k$로 나누어 데이터의 분포를 고르게 만드는 과정이고요. Masking은 말씀드린대로 $W$ 행렬과 행렬곱하는 과정인데요. 이 Masking 과정의 의미를 좀더 깊숙히 살펴보겠습니다.

$W = \left[ \begin{matrix} 1 & 0 & 0 & 0 & \cdots & 0 \\ 1/2 & 1/2 & 0 & 0 & \cdots & 0 \\ 1/3 & 1/3 & 1/3 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1/T & 1/T & 1/T & 1/T & \cdots & 1/T \end{matrix} \right]$

$y = Softmax(W \cdot \frac{Q \cdot K^T}{\sqrt{d_k}})\cdot V$ Masked Scaled Dot-Product Attention 함수식에서 Masking에 해당하는 부분만 보겠습니다. 바로 $W \cdot \frac{Q \cdot K^T}{\sqrt{d_k}}$ 부분인데요. $W$의 우삼각행렬이 모두 0으로 채워졌으며 각 행의 합은 1이라는 점이 핵심입니다.

앞서 $\frac{Q \cdot K^T}{\sqrt{d_k}}$의 (i, j) 칸에는 i번째 토큰과 관련된 예측을 하고자 할 때 j번째 토큰에 얼마나 주목(Attention)할지를 나타내는 값이 들어간다고 말씀드렸습니다. 그렇다면 $W \cdot \frac{Q \cdot K^T}{\sqrt{d_k}}$의 (i, j) 칸에 들어가는 값은 어떻게 해석할 수 있을까요? $W \cdot \frac{Q \cdot K^T}{\sqrt{d_k}}$의 (i, j) 칸에는 1번째 토큰부터 i번째 토큰까지 i개의 토큰 각각에 관한 예측을 하려고 할 때 j번째 토큰에 주목(Attention)할 정도의 평균값이 들어갑니다.

따라서 $\frac{Q \cdot K^T}{\sqrt{d_k}}$의 i번째 행벡터는 i번째 토큰과 관련된 예측을 하고자 할 때 각 토큰에 얼마나 주목할지를 나타낸다고 볼 수 있고요. $W \cdot \frac{Q \cdot K^T}{\sqrt{d_k}}$ 의 i번째 행벡터는, 1~i번째 토큰과 관련된 예측을 하고자 할 때 각 토큰에 주목하는 정도의 평균값을 나타낸다고 볼 수 있겠죠. $W \cdot \frac{Q \cdot K^T}{\sqrt{d_k}}$의 i번째 행벡터는 $\frac{Q \cdot K^T}{\sqrt{d_k}}$의 1-i번째 행벡터들의 평균이니까요. 이렇게 하면 추후에 Attention Value 행벡터들로 이루어진 행렬을 계산할 때 각 시점에서의 Attention Value는 이전 시점까지에 관한 정보만을 이용해서 구해지게 됩니다.

이를 Softmax 함수로 처리해주고 나면 모든 행의 합이 각각 1이 될 것인데요. Softmax는 각 토큰에 주목할 정도를 나타내는 값을 좀 더 고르게 만들어주는 동시에 총합이 1이 되도록 해줍니다. Softmax까지 거치고 나면 각 토큰의 Attention Value를 구할 때 다른 토큰의 밸류에 얼마나 주목할지를 나타내는 가중치 행렬이 완성됩니다.

마지막으로 앞에서 구한 (T, T) 가중치 행렬과 Value 행렬의 행렬곱을 통해 Attention Value 행렬을 구할 차례입니다. 아래 그림은 이 모든 과정을 포괄하는 그림입니다.

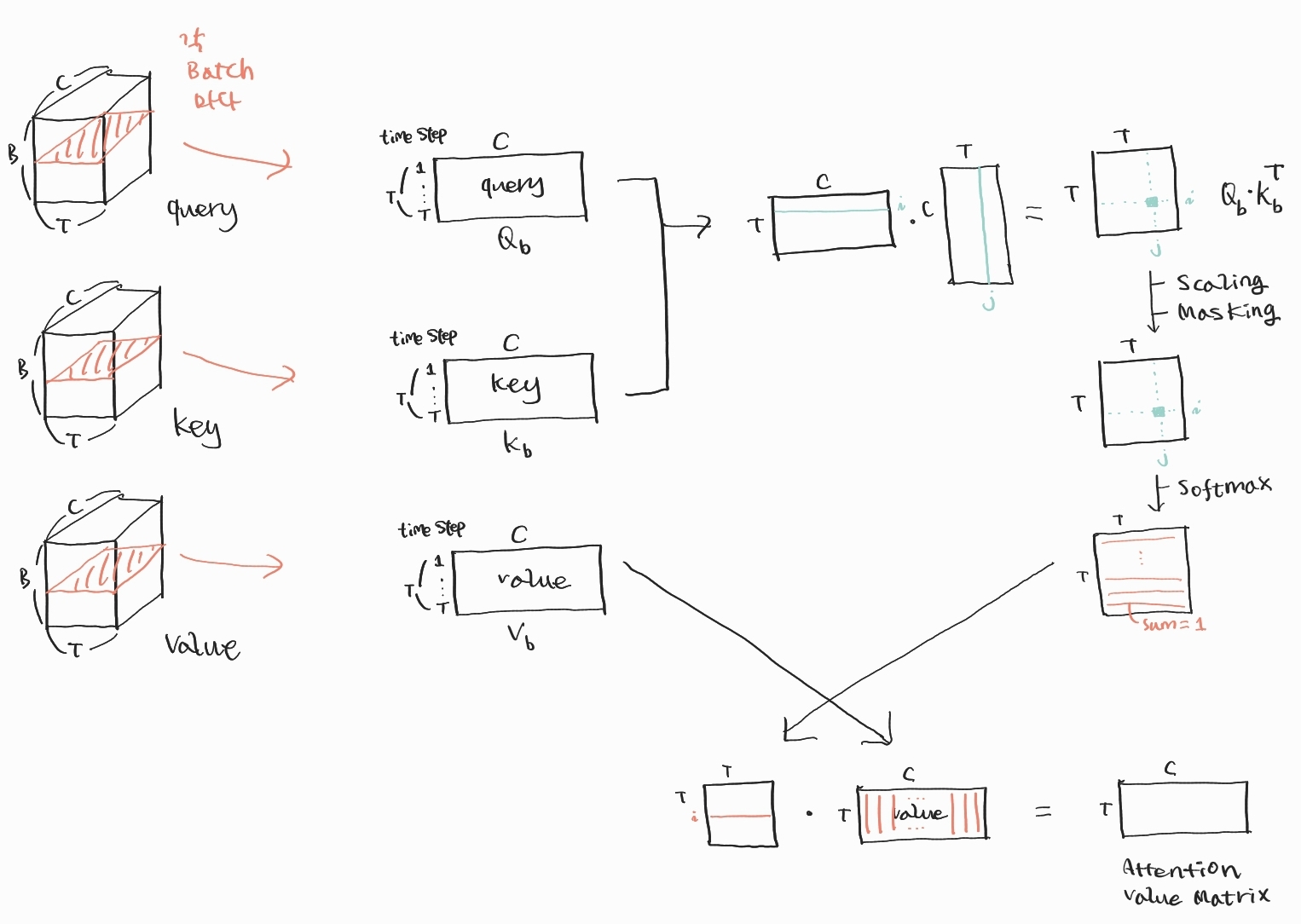
이 마지막 과정을 보면, (T, T) 가중치 행렬이 각 토큰의 Attention Value를 구할 때 다른 토큰의 밸류에 얼마나 주목할지를 나타낸다는 이야기를 이해할 수 있습니다. 밸류 행렬의 각 행벡터는 각 토큰의 밸류이므로, 이를 (T, T) 가중치 행렬에 행렬곱해주면, 각 토큰의 밸류를 가중합하게 되는 것입니다.

각 배치별로 이러한 Attention Value 행렬을 구하고, B개의 Attention Value 행렬을 쌓아주면 (B, T, C)의 크기를 가지는 Attention 함수의 출력값이 완성됩니다. 지금까지 각 배치에서 어떤 동작이 발생하는지를 따로 살펴봤는데요, 공부하려고 한 번 쪼개어 본 것 뿐이고요. 배치에 따라 쪼갤 필요 없이 (B, T, C) 행렬 통째로 계산해도 같은 연산이 일어납니다.

마무리

Self-Attention 연산에 관한 내용은 여기까지 하겠습니다. 지금까지 보여드린 그림들 중 아래에 다시 첨부한 두 개의 그림이면 전체 과정을 포괄할 수 있습니다.

위 그림에서 Attention Function 내부를 들여다 보면 아래 그림들과 같습니다!

먼저 Masking을 거치지 않는 버전

Masking을 거치는 버전

그럼 다음번 글에서는 Multi-Head Attention에 관해 알아보겠습니다!